5.2 Nullstellen quadratischer Funktionen
Es gibt Methoden, die man bei jeder quadratischen Funktion anwenden kann, um sie zu lösen. Diese sind die "p-q-Formel", die "Mitternachtsformel" oder die "quadratische Ergänzung". Allerdings sind all diese Lösungswege etwas kompliziert. Daher lohnt es sich zuerst die Sonderfälle zu betrachten, bei denen es einfachere Lösungswege gibt.
Das Berechnen von Nullstellen einer Funktion beginnt immer damit, dass man die Funktionsgleichung gleich Null setzt!!
Der einfachste Fall ist der, bei dem man einfach Wurzeln ziehen kann:
5.2.1 Nullstellen berechnen durch Wurzel ziehen
Diese Methode eignet sich für alle quadratischen Funktionen, in denen kein x ohne Exponent vorkommt. Diese haben die Form: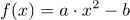 
Zu lösen ist also: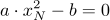 
. Hier steht der Index "N" an dem x, weil diese Gleichung nur noch eine richtige Aussage ist, wenn das x eine Nullstelle ist.
+Zahlenbeispiele 1
Für die nächsten beiden Fälle brauchen wir den
Satz vom Nullprodukt
Ein Produkt P=a · b · c ... ist genau dann gleich Null, wenn mindestens einer der Faktoren a, b ... gleich Null ist.
5.2.2 Nullstellen berechnen durch ausklammern
Wenn jeder Summand der Funktion die Variable x ebthält, dann kann man ein x ausklammern. Funktionen, auf die das zutrifft, haben die Form:
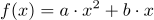
zu lösen ist also
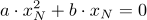
Hier lässt sich ein x ausklammern
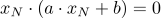
Dieses Produkt ist also genau dann gleich Null, wenn xN gleich Null ist oder wenn der Inhalt der Klammer gleich Null ist. In einem slochen Fall ist also immer eine Nullstelle xN1=0 und die zweite erhält man, indem man die Klammer gleich Null setzt und nach x auflöst, also a · xN2 + b = 0.
+Zahlenbeispiel 2
5.2.3 Nullstellen berechnen, bei einer Linearfaktordarstellung
Eine Klammer der Form (x-a) nennt man einen Linearfaktor. Dabei kann das a eine beliebige Zahl sein. Eine quadratische Funktion in Linearfaktordarstellung hat die Form:
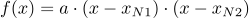
Zu lösen ist also: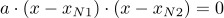 
Nach dem Satz vom Nullprodukt ist die Gleichung oben genau dann gleich Null, wenn eine der beiden Klammern gleich Null ist. Es lässt sich leicht sehen, dass das genau dann der Fall ist, wenn x = xN1 und wenn x=xN2.
Zahlenbeispiel:
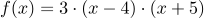
Hier kann man die Nullstellen sofort ablesen, nämlich xN1=4 und xN2=-5 .
Die Nullstellen sind also die Zahlen in den Linearfaktoren mit umgekehrtem Vorzeichen.
5.2.4 Allgemeine Formeln zum Berechnen von Nullstellen quadratischer Funktionen
Es gibt drei allgemeine Methoden, quadratische Gleichungen zu lösen:
5.2.4.1 Die p-q-Formel
Die p-q-Formel ist etwas gefährlich, weil mn bei ihrer Nutzung zu Flüchtigkeitsfehlern neigt. Trotzdem wird sie am meisten verwendet: Wenn eine Quadratische Gleichung gegeben ist, dann muss diese zuerst normiert werden, dass heißt vor dem x2 darf keine Zahl und auch kein Minuszeichen stehen: Die Ausgangsgleichung für die p-q-Formel hat daher immer die Form: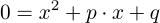 
Wenn eine quadratische Gleichung in dieser normierten Form vorliegt, aber erst dann(!), können p und q abgelesen werden und in die p-q-Formel eingesetzt werden:
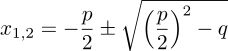
Das ergibt dann entweder zwei verschiedene, zwei gleiche oder keine Lösung
+Beispiele für die p-q-Formel
5.2.4.2 Die Mitternachtsformel
Die Mitternachtsformel trägt ihren Namen, weil frühere Pädagogen der Meinung waren, man müsse seine Schülerinnen und Schüler mitten in der Nacht wecken und nach dieser Formel fragen können und sie müssten wie aus der Pistole geschossen die Antwort kennen. Bei der Mitternachtsformel braucht nicht normiert zu werden. Die Ausgangsgleichung für die Mitternachtsformel hat daher die Form:
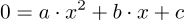
Dies brachte ihr in manchen Büchern auch den Namen abc-Formel ein. Die Formel lautet:
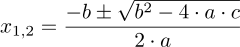
+Zahlenbeispiel für die Mitternachtsformel
5.2.4.3 Die quadratische Ergänzung
Mit der quadratischen Ergänzung kann man - mit Hilfe der binomischen Formeln - die p-q-Formel oder die Mitternachtsformel herleiten:
Beginnend mit einer normierten Gleichung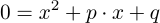 
und der Ergänzung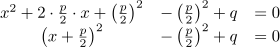 
Auflösen nach x ergibt die p-q-Formel:
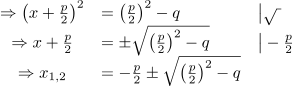
Ausführlichere Darstellung mit Zahlenbeispiel: ( pdf )
— zurück —