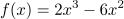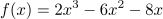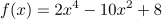[ Vorherige ] [ Weiter ]

5.3 Nullstellen bei Funktionen mit größerem Grad als 2

Eine exakte Lösung zur Berechnung von Nullstellen gibt es nur für lineare Funktionen un für quadratische Funktionen. Für ganzrationale Funktionen höheren Grades als 2 gibt es nur in Sonderfällen die Möglichkeit, Nullstellen exakt zu berechnen.

5.3.1. Ausklammern

In einigen Fällen lassen sich ein oder mehrere x ausklammern. Dann ist auf jeden Fall eine Nullstelle schon gleich Null. Wenn in der Klammer eine lineare oder eine quadratische Funktion übrig bleibt, dann können auch alle anderen Nullstellen bestimmt werden:

Beispiele

Hier kann 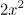ausgeklammert werden: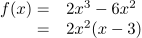
Aus dem Satz vom Nullprodukt lernt man, dass f(x) genau dann Null ist, wenn 2·x2 oder wenn (x-3) gleich Null ist. Nun lassen sich die Nullstellen leicht ablesen: 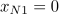, wie immer, wenn ein x ausgeklammert werden kann und die zweite Nullstelle ist das x, für das die Klammer zu Null wird, also .

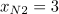Hier kann 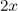ausgeklammert werden: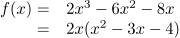
Nach dem Satz vom Nullprodukt ist wieder xN1=0. Für die anderen Nullstellen muss berechnet werden, für welche x die Klammer Null wird. Dies gelingt mit der p-q-Formel, da in der Klammer eine normierte quadratische Funktionsgleichung steht. (xN2=-1 und xN3=4, probieren Sie es aus)

5.3.2. Nullstellen bei einer Linearfaktordarstellung

Ist die ganzrationale Funktion in einer Linearfaktordarstellung gegeben, dann kann man die Nullstellen einfach ablesen. Wenn eine der Klammern gleich Null ist, dann ist die ganze Funktionsgleichung gleich Null. Auch dies ist eine Anwendung des Satzes vom Nullprodukt. Und es lässt sich mit einem Blick sehen, welches x in eine der Klammern eingesetzt werden muss, damit diese zu Null wird:

Beispiel: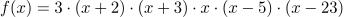

Hier lauten die Nullstellen xN1=-2, xN2=-3, xN3=0, xN4=5, xN5=23
Wenn eine Funktionsgleichung in Linearfaktordarstellung gegeben ist, lassen sich die Nullstellen also sofort ablesen. Nur vorsicht: Es ist die Zahl aus der Klammer mit umgekehrtem Vorzeichen!! Wenn ein x ohne Klammer als Faktor dabei ist, dann ist eine Nullstelle die Null.

5.3.3. Nullstellen berechnen mit Substitution

Manchmal hilft es, einen Wiederkehrenden Teil der Funktionsgleichung zu substituieren, also durch einer anderen Variable zu ersetzen:
Beispiele:

Da x4=(x2)2 ist, kann man in dieser Gleichung x2 durch einen anderen Buchstaben ersetzen, zum Beispiel u=x2.
Dann lautet die Funktionsgleichung: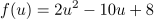
Dieses ist wieder eine quadratische Gleichung, die mit den bekannten Methoden aus 5.2 gelöst werden kann. Man erhät zum Beispiel mit der Mitternachtsformel:

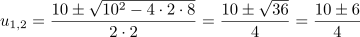
Also ist 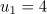und .
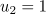Rücksubstitution: Nun müssen wir uns daran erinnern, dass u=x2 ist: Also gilt

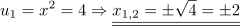
und

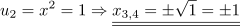
Es gibt also vier verschiedene Nullstellen.

  1. Bei der Funktion 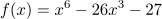kann man u=x3 substituieren.

Vorsicht: Beim Rücksubstituieren sind - im Gegensatz zur Quadratwurzel - beim Ziehen der dritten Wurzel aus u auch negative Zahlen in der Wurzel möglich. Dafür gibt es jeweils nur eine Lösung pro Wurzel!
Mit folgt und
Rücksubstitution: Dann ist 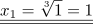und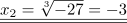

5.3.4. Polynomdivision

Satz vom Faktorisieren

Gegeben ist eine ganzrationale Funktion f(x) n-ten Grades und eine Nullstelle dieser Funktion xN.
Dann gibt es eine andere ganzrationale Funktion g(x) vom Grad n-1, für die gilt:
f(x)=(x-xN) · g(x)

Bemerkung: Diese Funktion g(x) kann man mit Hife einer Polynomdivision ausrechnen

Das Verfahren der Polynomdivision

Wenn eine Funktion f(x) dritten Grades gegeben ist, und eine Nullstelle bekannt ist, dann kann nach dem Satz vom Faktorisieren eine Funktion g(x) gefunden werden, mit f(x)=(x-xN) · g(x)
g(x) ist dann eine Funktion zweiten Grades und die Nullstellen dieser Funktion können mit Hilfe der Methoden aus 5.2 berechnet werden.
Um g(x) zu finden, müssen wir eine Polynomdivision berechnen: g(x)=f(x):(x-xN)
Die Polynomdivision lässt sich wie eine "traditionelle" Division oder mit Hilfe des Horner-Schemas durchführen.
Die Rechnung mit dem Hornerschema ist oft die einfachere Lösung: (pdf)

Ist die Funktion f(x) vierten Grades, dann müssen schon zwei Nullstellen bekannt sein. Dann muss zweimal hintereinander eine Poynomdivision durchgeführt werden.

Übungsaufgaben zur Polynomdivision mit Lösungen (pdf)

Sind alle Nullstellen bekannt, dann kann die Funktion f(x) als Linearfaktordarstellung geschieben werden:
f(x)=an · (x-xN1) · (x-xN2) · ...
Das an ist der Leitkoeffizient aus der Polynomdarstellung der ganzrationalen Funktion f(x)= an · xn + an-1 · xn-1 + ... + a0

— zurück —