7 Anwendungen der Differentialrechnung
Kapitel:
- Berechnen von Steigungen eines Funktionsgraphen an einer Stelle x = c
+7.2 Berechnung von Krümmungen eines Funktionsgraphen an einer Stelle x = c
+7.3 Berechnen von Extrempunkten
+7.4 Berechnen von Wende- und Sattelpunkten
+7.5 Funktionssynthese - Einführung
+7.6 Funktionssynthese für Fortgeschrittene
+7.7 Trassierungen
7.1 Berechnen von Steigungen eines Funktionsgraphen an einer Stelle x = c
Eigentlich ist die Differentialrechnung genau dafür gemacht. Mit Hilfe der Ableitungsfunktion f'(x) lässt sich an jeder Stelle x berechnen, wie steil der Funktionsgraph hier nach oben oder nach unten geht.
7.1.1 Darstellungen von Steigungen
Steigungen können in unterschiedlicher Weise gemessen oder beschrieben werden.
- als Dezimalzahl: Dieses ist in der Mathematik die übliche Beschreibung. Bei den linearen Funktionen erhält man die Dezimalzahl über den Differenzenquotienten, bei allen anderen Funktionen mit hilfe des Differentialquotienten.
- in Prozent: Dies ist die übliche Beschreibung im Straßenverkehr: Wie viel Meter Höhe gewinnt oder verliert man auf eine horizontalen Strecke von 100 Metern.
- als Winkel: Dies ist im Abschnitt 4 über lineare Funktionen beschrieben ( → ). Für den Steigungswinkel an einer Stelle

gilt: 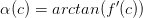 und umgekehrt:
und umgekehrt: 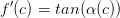 Dabei ist der WInkel α immer der Winkel des Graphen zur x-Achse.
Dabei ist der WInkel α immer der Winkel des Graphen zur x-Achse.
7.1.2 Die Bedeutung von Ableitungen bzw. von Steigungen in Aufgaben im Anwendungsbezug
Die Ableitung einer Funktion an einer Stelle x=c, also f'(c), ist mathematisch gesehen die Tangentensteigung an dieser Stelle. Grundsätzlich hat die Ableitung die Bedeutung einer Änderung oder Änderungsrate.
Immer wenn danach gefragt ist, wie schnell oder wie stark sich Funktionswerte ändern, dann ist nach der Ableitung gefragt.
7.1.3 Die Einheit von Steigungen
Da die Steigung mit einem Steigungsdreieck als 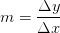 berechnet werden kann, ist die Einheit der Steigung grundsätzlich die Einheit der Größe die von der Ordinate beschrieben wird, durch die Einheit der Abszisse.
berechnet werden kann, ist die Einheit der Steigung grundsätzlich die Einheit der Größe die von der Ordinate beschrieben wird, durch die Einheit der Abszisse.
Beispiele:
- T(t) sei eine Funktion, die die Temperatur in Abhängigkeit von der Zeit in Stunden beschreibt. Wenn die Temperatur T in Grad Celsius und die Zeit in Stunden angegeben ist, dann ist die Einheit der Funktionswerte der Ableitungsfunktion Grad Celsius pro Stunde
- P(h) sei eine Funktion, die den Luftdruck in Abhängigkeit von der Höhe beschreibt. Wird der Druck in Pascal und die Höhe in Kilometern angegeben, dann ist die Einheit der Funktionswerte der Ableitungsfunktion Pascal pro Kilometer, also
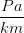
Aufgaben
Aufgaben mit Anwendungsbezug ( pdf )
