7.6 Funktionssynthese für Fortgeschrittene

Viele weitere Bedingungen sind möglich

Bisher haben wir in einem Beispiel eine Funktion bestimmt, die durch drei vorgegebene Punkte geht. Aber es gibt viele weitere Eigenschaften, die zu einer Bedingung gemacht werden können:
Dazu müssen alerdings auch die Ableitungen unseres Prptotyps gebildet werden.
Nehmen wir an, gesucht ist eine Funktion dritten Grades, dann lauten die Prototypen für f, f' und f'':

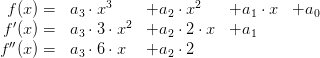
Dann sind noch folgende Nebenbedingungen möglich: (Nebenbedingungen als pdf-Datei)

Dabei muss beachtet werden:

• Immer wenn in einer Aufgabe nach einer extremen Änderung gefragt ist, dann ist ein Wendepunkte gemeint. Also notwendige Bedingung f''(x)=0
• Immer eine Änderungsrate oder eine Betrag für eine Änderung gegeben ist, dann ist der Funktionswert der ersten Ableitungtsfunktion gemeint

Beispiel (pdf)

Mögliche Nebenbedingungen

A) Ein Punkt P(px|py) liegt auf dem Funktionsgraphen der Funktion f(x)

Mathmatisch heißt das, dass die Punktprobe mit dem Punkt P erfüllt sein muss: py = f( px )

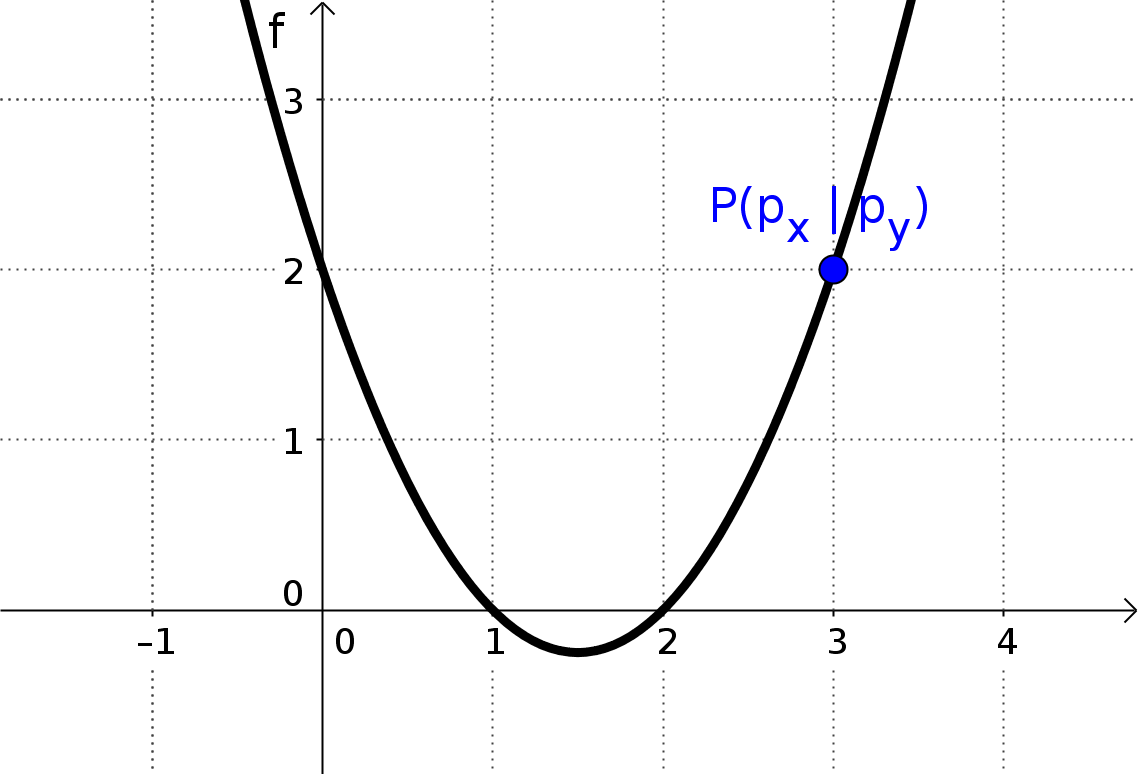
Zahlenbeispiel: Punkt P(3|2) und Funktion f(x) also muss die Bedingung gelten: f(3)=2

B) Der Funktionsgraph von f(x) hat an der Stelle a die Steigung b

Da die erste Ableitungsfunktion die Tangentensteigung der Funktion f(x) wiedergibt, lautet die Bedingung: f'(a) = b

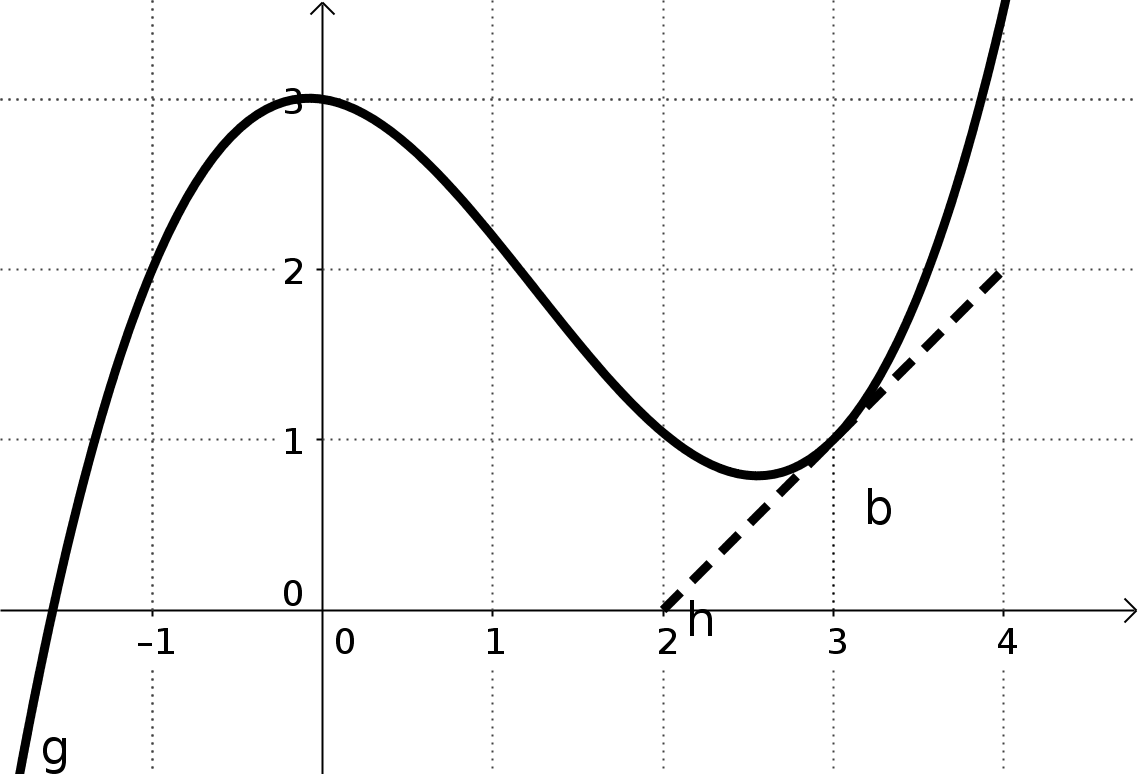
Zahlenbeispiel: Beispiel: An der Stelle x=3 die Steigung 1, also f'(3)=1

C) Der Funktionsgraph von f(x) hat an der Stelle x=a ein Extremum

Die Notwendige Bedingung zur Berechnung einer Extremstelle: f'(a) = 0

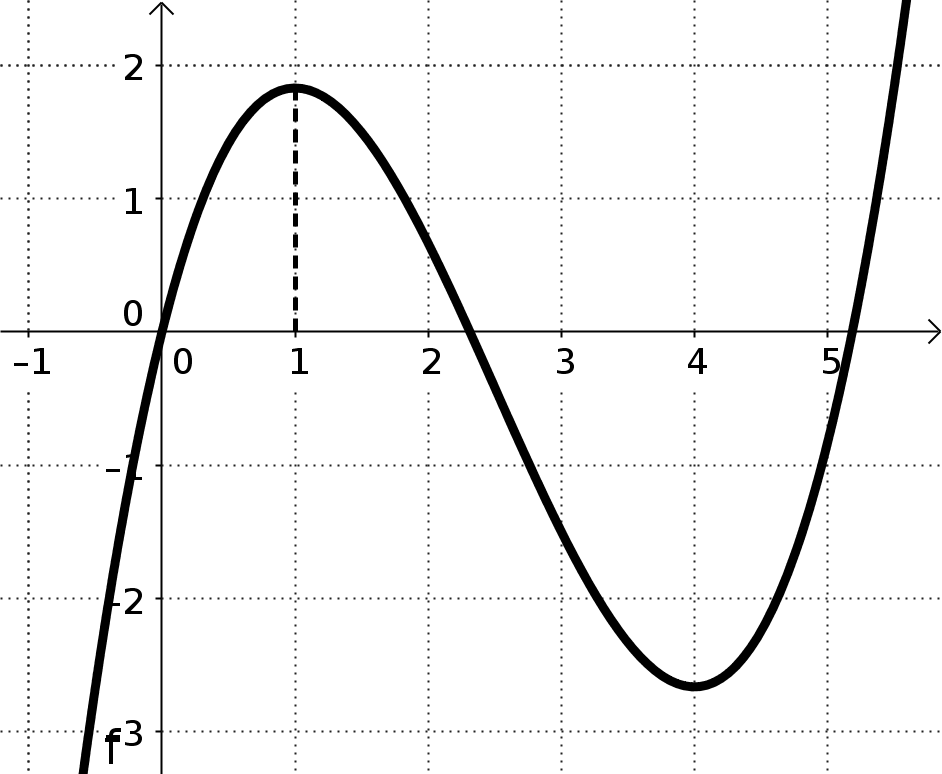
Zahlenbeispiel: f(x) hat einen Hochpunkt bei x = 1: f'(1) = 0

D) Der Funktionsgraph von f(x) hat an der Stelle x=a einen Wendepunkt

Die Notwendige Bedingung zur Berechnung einer Wendestelle: f''(a) = 0

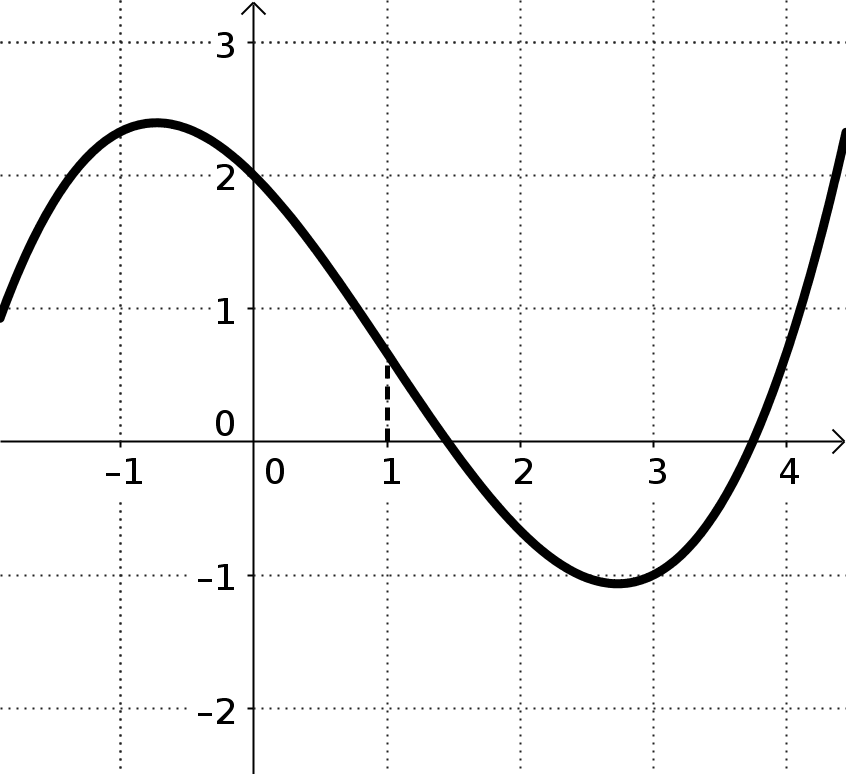
Zahlenbeispiel: f(x) hat einen Wendepunkt bei x = 1: f'(1) = 0
oder: Die Steigung von f(x) hat bei x=1 einen Tiefpunkt (hier geht es "am steilsten nach unten")

E) Der Funktionsgraph von f(x) hat im Punkt P(px|py) einen Extrempunkt

Hinter dieser Bedingung stecken gleich zwei mathematische Bedingungen, nämlich A) und C), also f(px) = py und f'(px) = 0

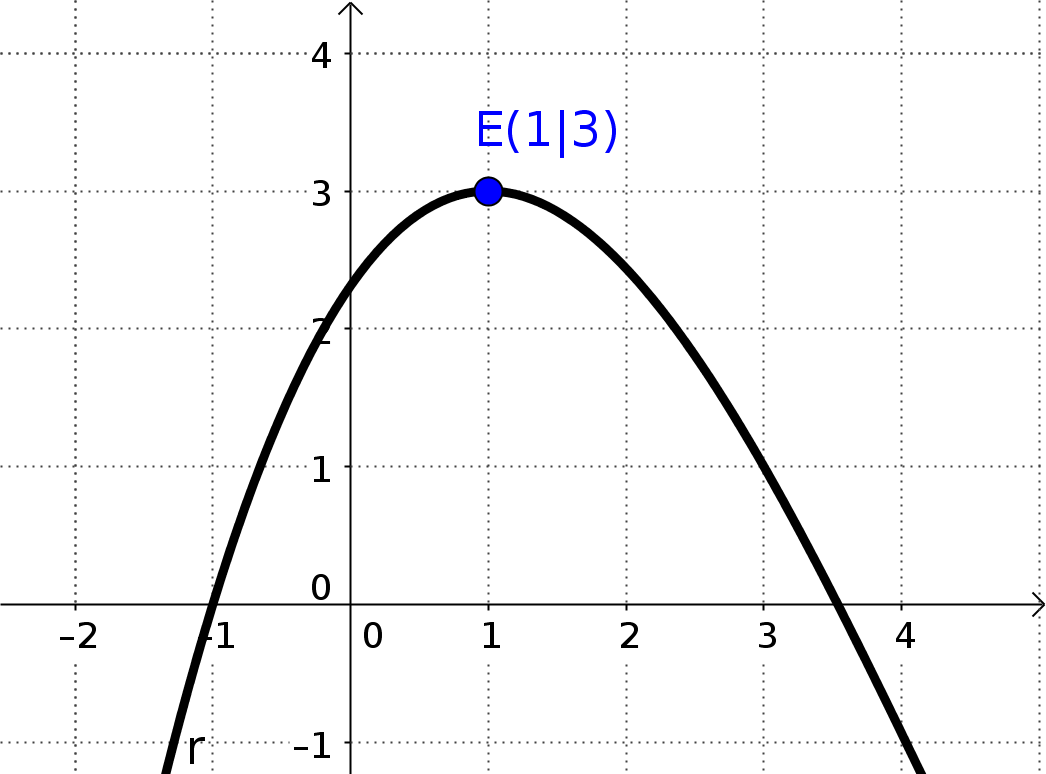
F) Der Funktionsgraph von f(x) hat im Punkt P(px|py) einen Wendepunkt

Hinter dieser Bedingung stecken gleich zwei mathematische Bedingungen, nämlich A) und D), also f(px) = py und f''(px) = 0

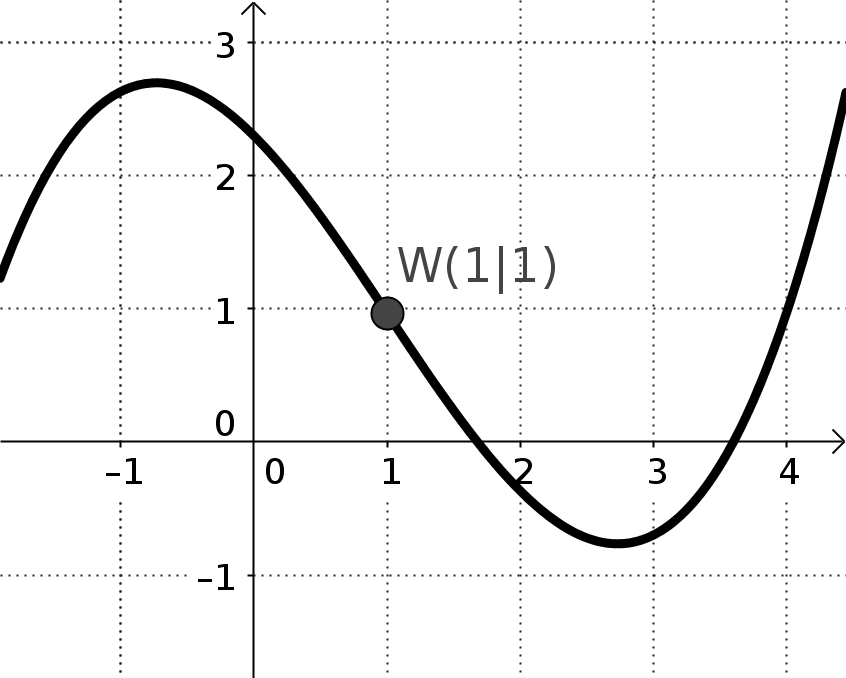
G) Der Funktionsgraph von f(x) hat im Punkt P(px|py) einen Sattelpunkt

In dieser Bedingung sind sogar drei Mathematische Bedingungen versteckt:
Der Funktionsgraph geht durch den Punkt: f(px) = py
Bei einem Sattelpunkt ist die Steigung gleich 0: f'(px) = 0
Ein Sattelpunkt ist ein Wendepunkt: f''(px) = 0

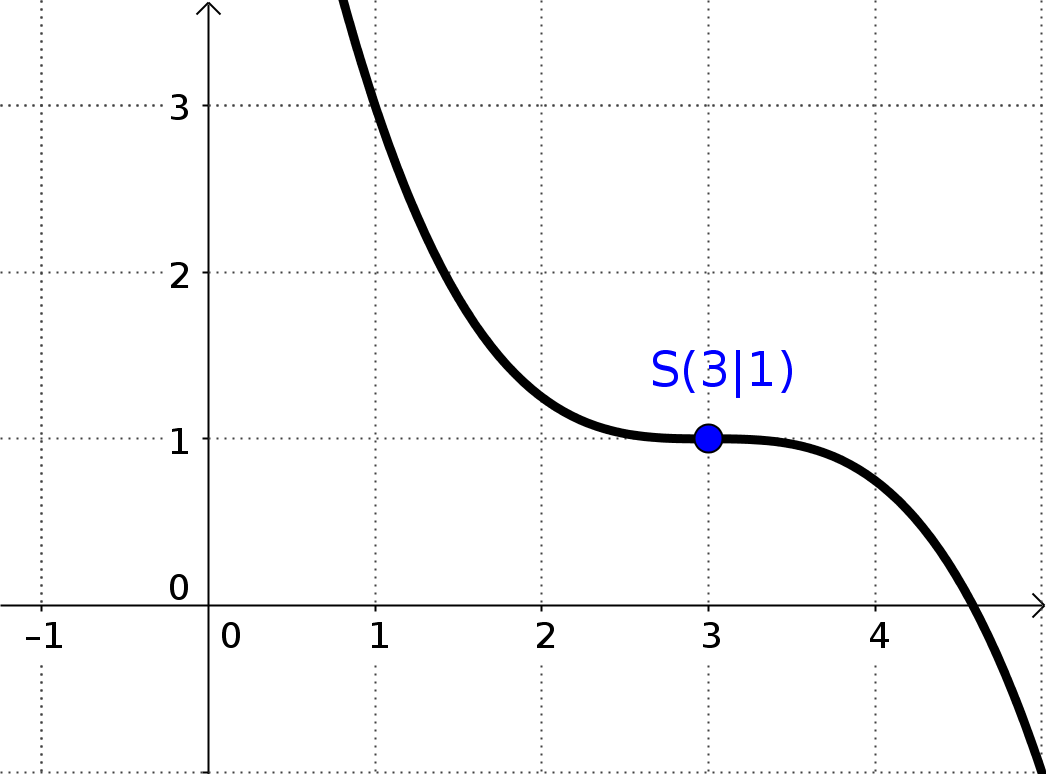
H) Der Funktionsgraph von f(x) schneidet den Funktionsgraphen von g(x) an der Stelle x=a

Mathematische Bedingung zur Berechnung einer Schnittstelle: f(a)=g(a)

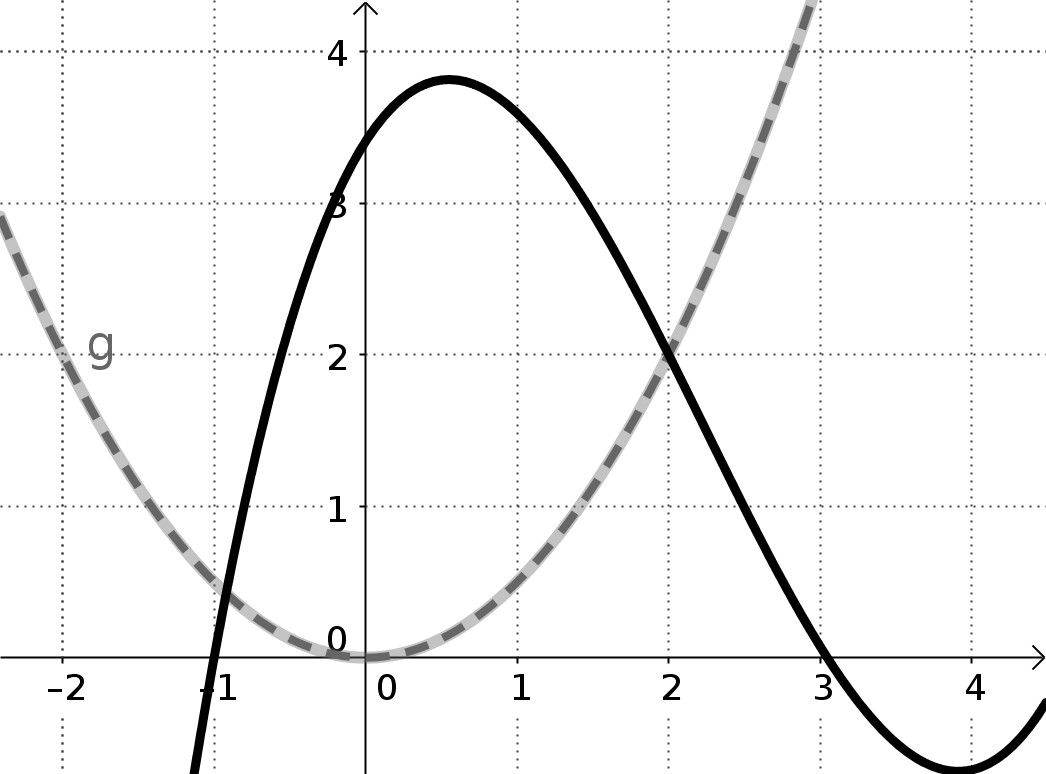
I) Der Funktionsgraph von f(x) schneidet den Funktionsgraphen von g(x) an der Stelle x=a senkrecht

Mathematische Bedingung zur Berechnung einer Schnittstelle: f(a)=g(a)
Bedingung für senkrechtes Schneiden: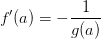
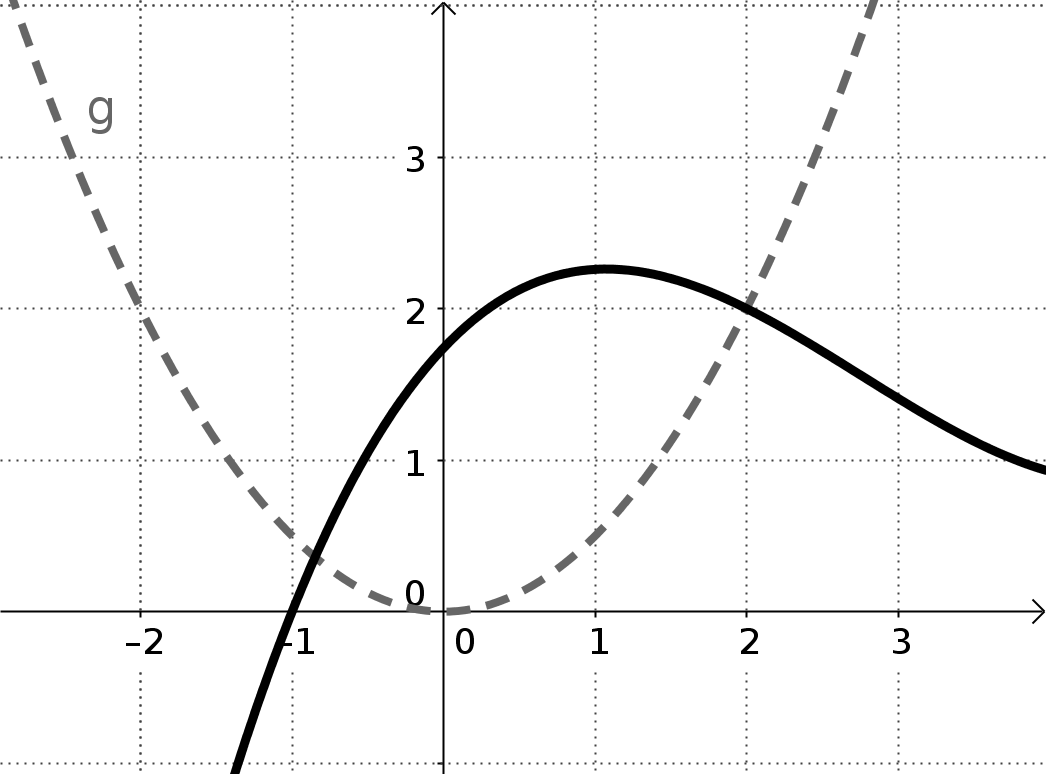a = 2

I) Der Funktionsgraph von f(x) berührt den Funktionsgraphen von g(x) an der Stelle x=a

Mathematische Bedingung zur Berechnung einer Schnittstelle: f(a) = g(a)
Bedingung für das Berühren (beide Graphen haben hier die gleiche Steigung): f'(a) = g'(a)
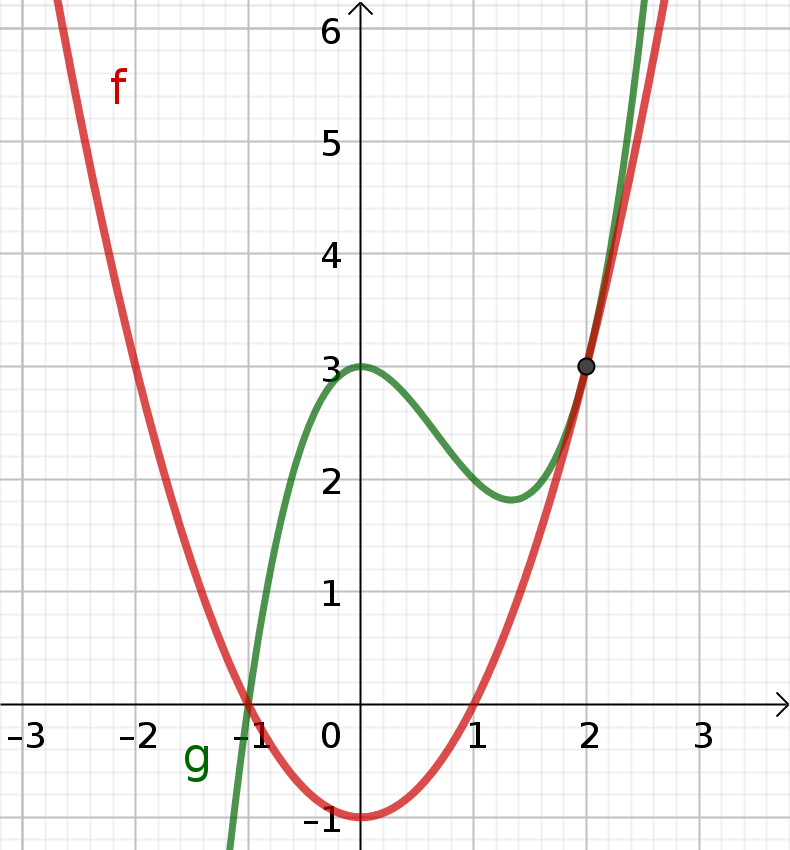a=2