7.5 Funktionssynthese - Einführung

Wo kommen die Funktionen her?

Bisher gab es immer einen "allmächtigen" Aufgabensteller, der behauptet hat, dass sich irgend etwas durch eine Funktionsgleichung beschreiben ließe. "Woher weiß der das?" Könnte man sich fragen, oder noch schlimmer: "Das stimmt doch ohnehin nicht." In diesem Kapitel geht es darum, wo diese Funktionen herkommen beziehungsweise, wie man sich Funktionen für Anwendungen "maßschneidern" kann.

7.5.1 Die Bedingungen an eine Funktion

Eine Funktion soll einen Sachverhalt beschreiben können. Eine Möglichkeit eine Funktion zu erzeugen ist es daher, ein Experiment zu machen, ein paar Messwerte zu finden, und sich dann zu überlegen, welche Funktionsgleichung diese Messwerte beschreiben kann:

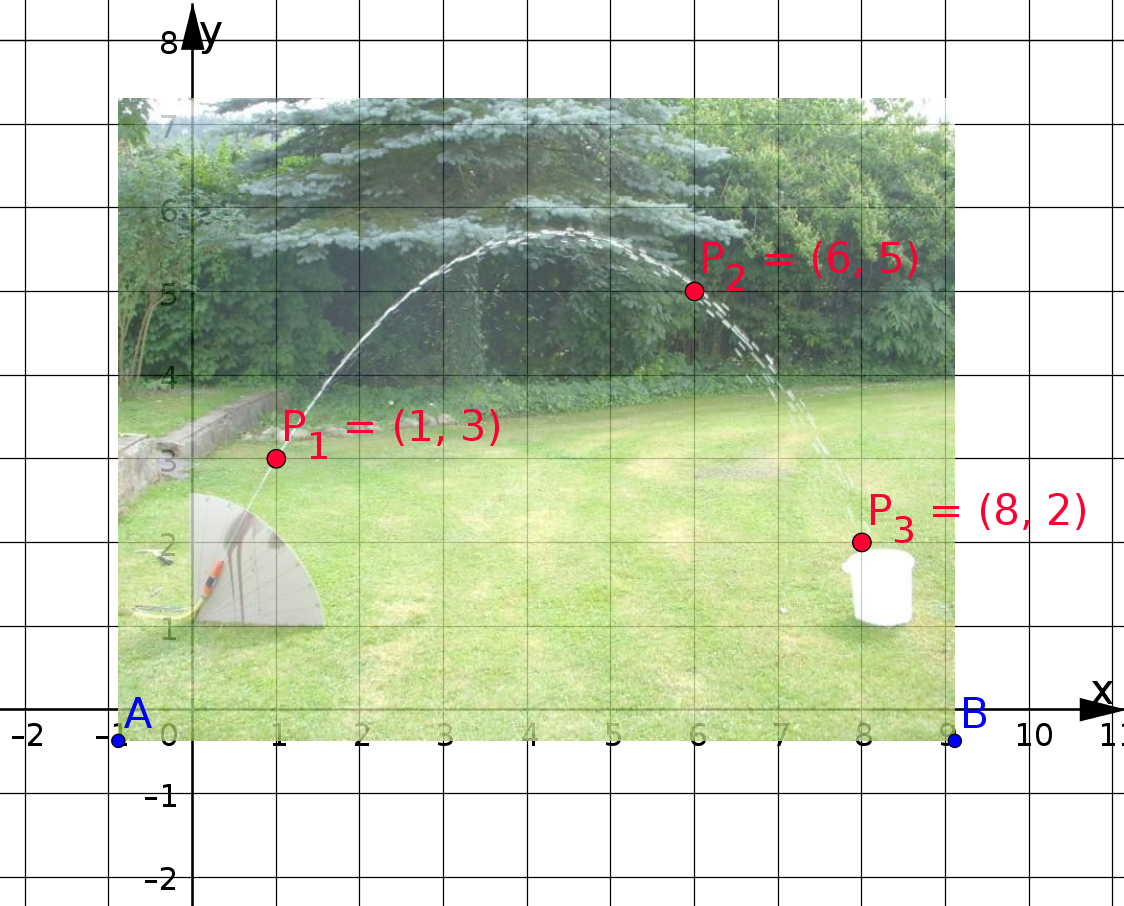
In der Abbildung ist ein Wasserstrahl abgebildet. Gesucht ist die Funktionsgleichung, die den Verlauf des Wasserstrahls beschreibt.
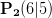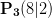Die Koordinaten der drei Punkte lauten: , und . Diese Punkte wurde deshalb ausgewählt, weil sich die Koordinaten mit ganzen Zahlen beschreiben lassen. Das erleichtert uns die Rechnung etwas.

7.5.2 Der Funktions-Prototyp

Bevor man mit einer Funktionssynthese beginnt, muss man schon eine Ahnung haben, wie die gesucht Funktionsgleichung ungefähr aussehen wird. Aus der Physik weiß man, dass solch ein Wasserstrahl entlang einer Wurfparabel verläuft. Es geht also um eine Parabel, eine ganzrationale Funktion zweiten Grades.
Alle ganzrationalen Funktionen zweiten Grades lassen sich in der Polynomdarstellung schreiben, als:

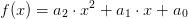
Wer mag kann als Namen für die Koeffizienten statt a₂, a₁ und a₀ auch einfach die Buchstaben a,b, und c wählen.
Diese Funktionsgleichung hat drei unbekannte Parameter, nämlich 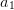, 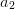und 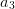. Um eine Lösung für diese Funktion zu finden, braucht man genau so viel Bedingungen, wie es unbekannte Parameter gibt.

7.5.3 Das Gleichungssystem

Aus den Bedingungen und dem Funktionsprototypen kann man nun ein Gleichungssystem für die Parameter 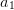, 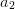und 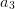erstellen:

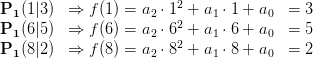
Wenn die Quadrate ausmultipliziert werden, dann erhät man das Gleichungssystem:

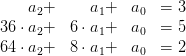
7.5.4 Lösen des Gleichungssystems

Nun gilt es Parameter 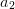, 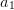und 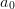zu finden, die jede der drei Gleichungen erfüllen. Dies ist der schwerste Teil der Aufgabe.
Die Lösungsverfahren, die auf dem Gauß-Algorithmus basieren, haben alle zum Ziel, das Gleichugnssystem so umzuwandeln, dass es eine Dreiecksform bildet:

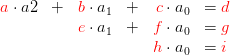
• Wenn das erreicht ist, dann ist es aus der untersten Gleichung ganz einfach, a₀ zu berechnen:
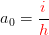
• Wenn dieses a₀ in die mittlere Gleichung eingesetzt wird, dann erhält man a₁.
• Wenn diese berechneten Werte für a₀ und a₁ in die oberste Gleichung eingesetzt werden, dann lässt sich auch a₂ berechnen.

Natürlich lässt sich das gleiche auch erreichen, wenn das Dreieck "anders herum" ist:

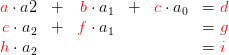
Um Gleichungssysteme umzuformen dürfen die Gleichungen auf drei Weisen verändert werden:

1. Eine gesamte Gleichungen darf mit einer beliebigen Zahl multipliziert werden
2. Eine Gleichung darf zu einer anderen Gleichung addiert oder von ihr subtrahiert werden
3. Gleichungen dürfen in der Reihenfolge vertrauscht werden

Die dritte Möglichkeit wird oft übersehen, kann aber manche Rechnungen sehr vereinfachen.

Anleitungen zur Lösung linearer Gleichungssysteme

Es gibt mehrere Möglichkeiten lineare Gleichungssysteme zu lösen. Einige sehen zwar beim Zusehen leicht aus, erfordern aber etws mathematische Intuition. Andere Rezepte sehen zuerst etwas komplizierter aus, dafür kann man immer nach der gleichen Methode vorgehen. Es empfiehlt sich, alle Lösungsmethoden gründlich auszuprobieren. Dabei lernt man auf der einen Seite viel über mathematische Grundlagen, auf der anderen Seite lassen sich die ideen sogar kombinieren. Am Ende reicht es allerdings, wenn man eine der Methoden sicher beherrscht.
Das wichtigste bei all diesen Lösungswegen ist, die Gleichungssysteme sauber und vollständig aufzuschreiben. Denn der häufigste Fehler dabei ist das versehentliche Vergessen eines Minuszeichens.

• Der herkömmliche Gauß-Algorithmus: (Standard-Gauß als pdf-Datei )
• Der "normierte" Gauß-Algorithmus: (Normierter Gauß als pdf-Datei)
• "Turbo-Gauß", vielleicht die schnellste Variante: (Turbo-Gauß als pdf-Datei)
• Lösung mit Determinanten: (Determinantenlösung als pdf-Datei)

Beispiel: Lösung des Gleichungssystems "normiert"

Zu lösen ist:

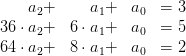
Schreiben des Systems als erweiterte Matrix und alle Gleichungen (Zeilen) bekommen einen Namen:

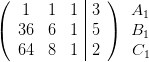
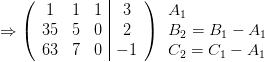
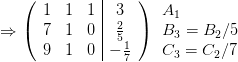
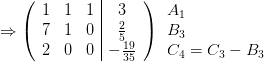
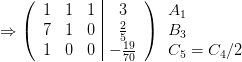Aus der letzten Zeile C₅ folgt: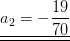
a₂ in B₃ einsetzen: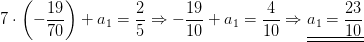
a₂ und a₁ in A₁ einsetzen: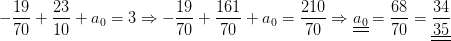
Damit lautet die gesuchte FUnktionsgleichung: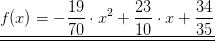

Probe: Punktprobe mit den oben ausgesuchten Punkten - Probieren Sie selbst: f(1)=3, f(6)=5 und f(8)=2

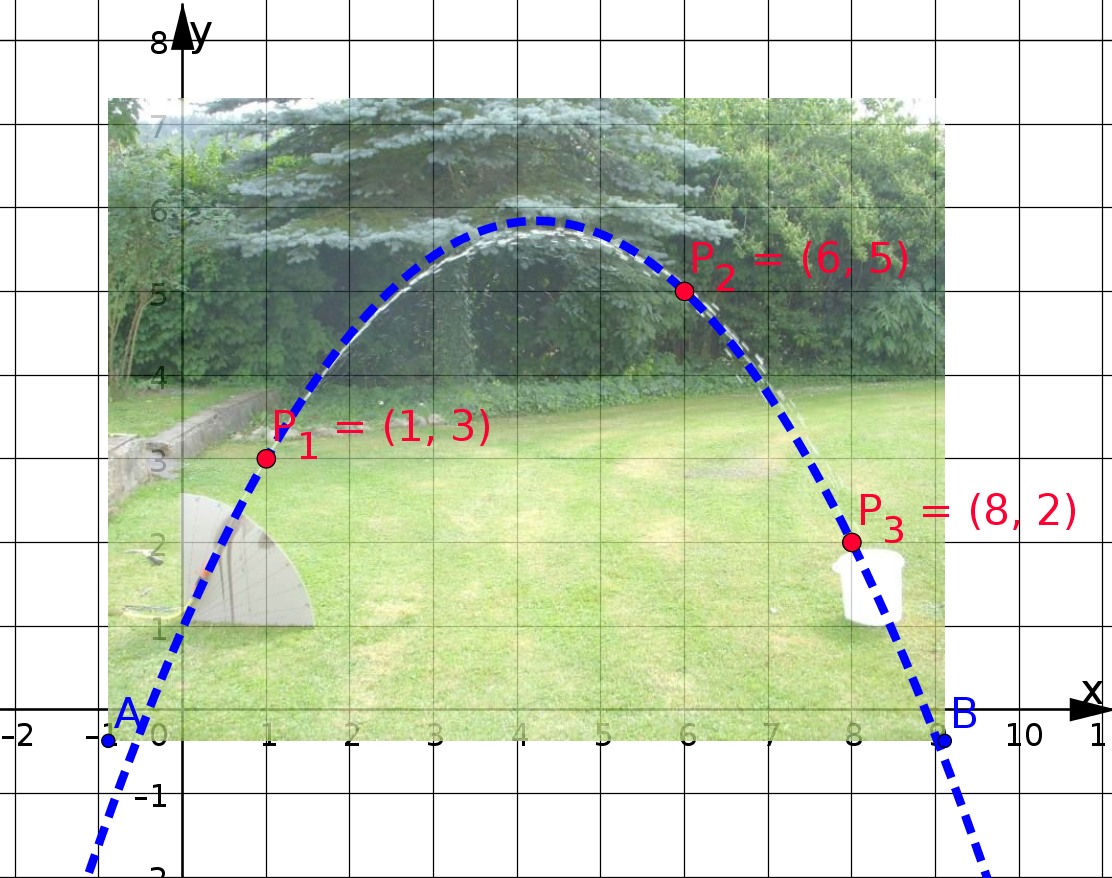
Einsetzen in Geogebra ergibt, dass die berechnete Funktion sehr genau auf den Wasserstrahl passt :-)