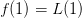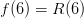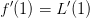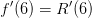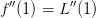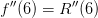7.7 Trassierungen
Eine Häufige Anwendung von Funktionssynthesen sind Trassierungen und sogenannte Splines. Beides führt darauf zurück, dass es links und rechts zwei Kurvenstücke gibt, die miteinander verbunden werden müssen.
Auch in der Computergrafik werden solche Systeme oft angewendet.
Bei der Trassierung geht es darum, z.B. Eisenbahnschienen oder Straßenstücke miteinander zu verbinden. Sehen Sie sich folgendes Problem an:
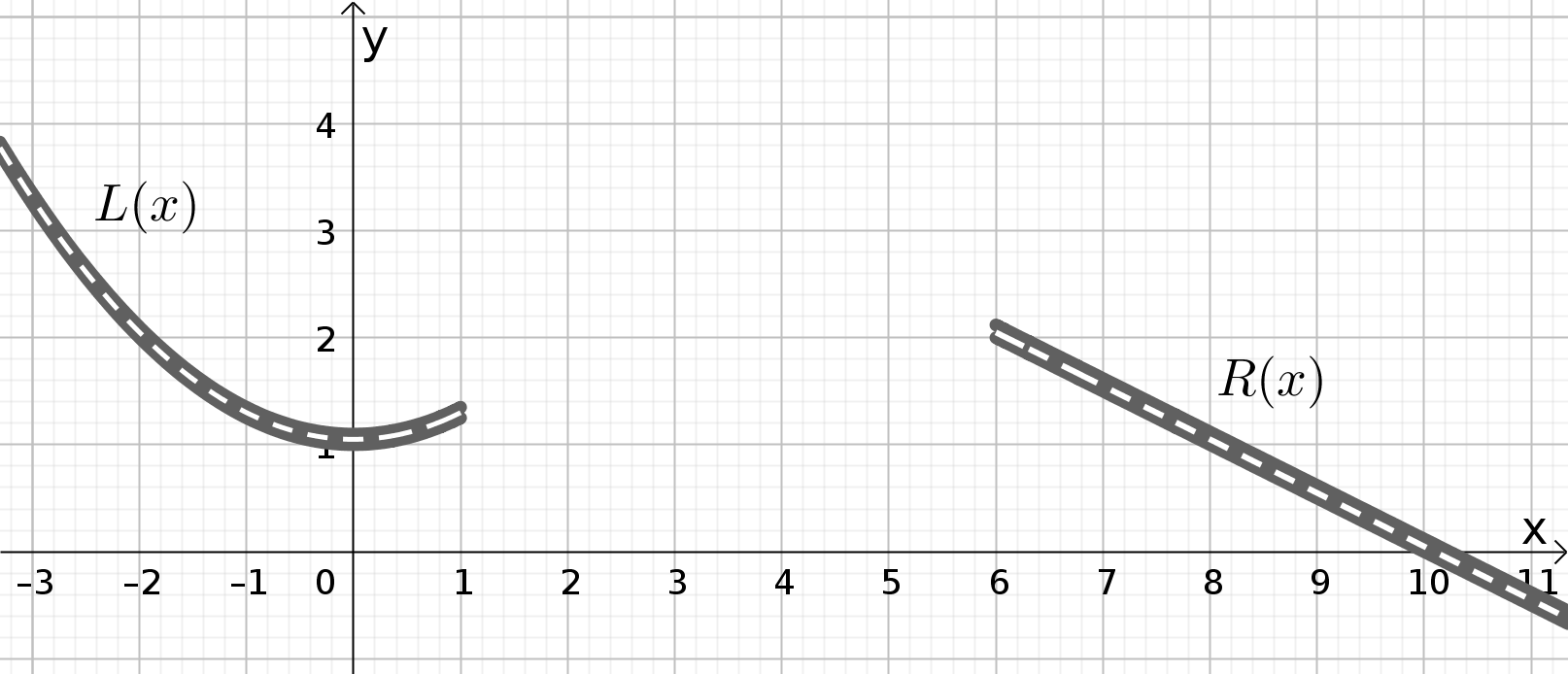
Das Straßenstück L(x) soll mit dem Straßenstück R(x) verbunden werden. Die Einheiten in Richtung x und y betragen hier 100 m pro Einheit.
Für einen sicheren Straßenverkehr müssen nun einige Bedingungen eingehalten werden:
Versatzfreiheit - Gleichsetzen der Funktionsgleichungen
Die Straßen müssen versatzfrei sein. Was heißt das? Das ist eigentlich so selbstverständlich, dass nicht-Mathematiker darüber wohl gar nicht nachdenken würden. Folgendes Straßenstück wird wohl keine gute Lösung sein:
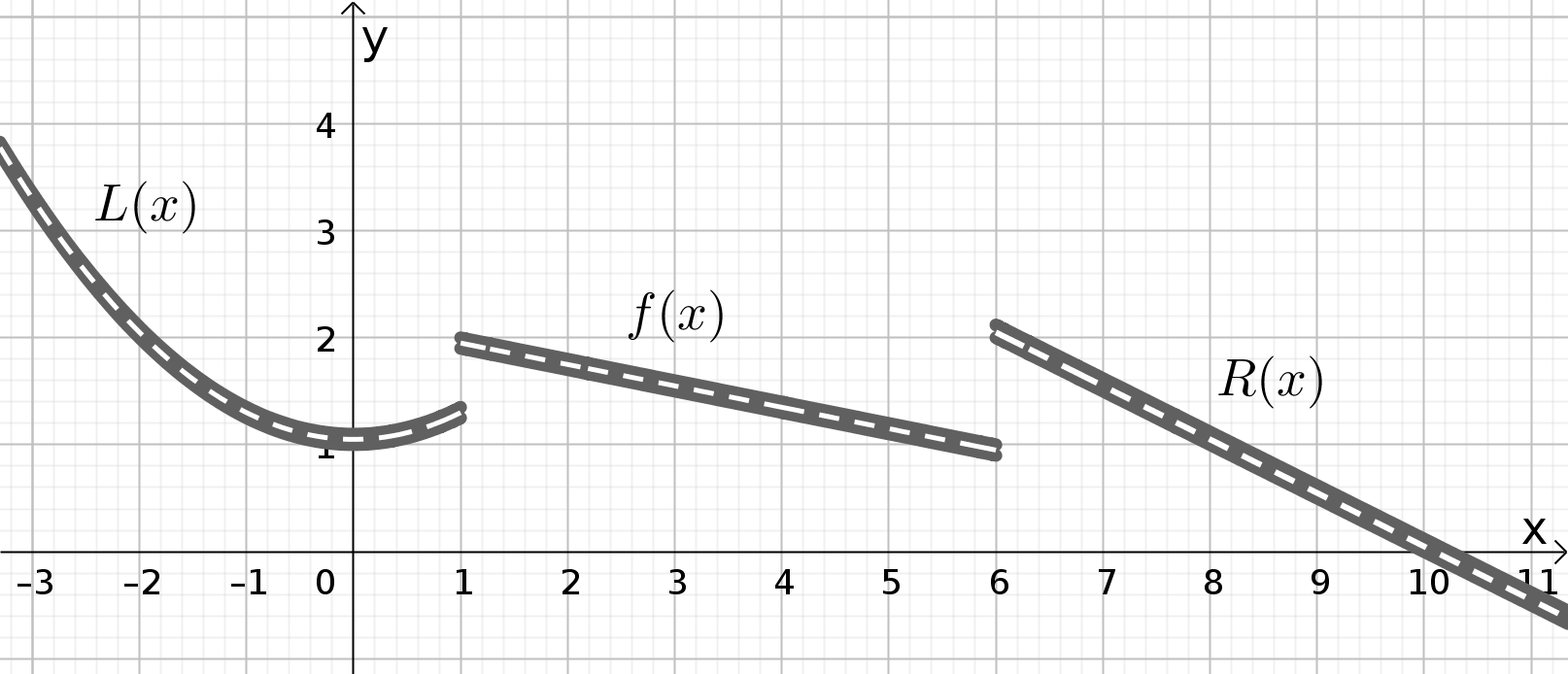
Warum nicht? Weil die Straßenstücke einen Versatz haben, sie beginnen nicht im gleichen Punkt.
Damit die Funktion f(x) die beiden Funktionen L(x) und R(x) gut miteinander verbindet, müssen die folgenden beiden Bedingungen erfüllt sein:
Wenn diese beiden Bedingungen erfüllt sind, dann könnte eine Verbindungsstraße zum Beispiel so aussehen:
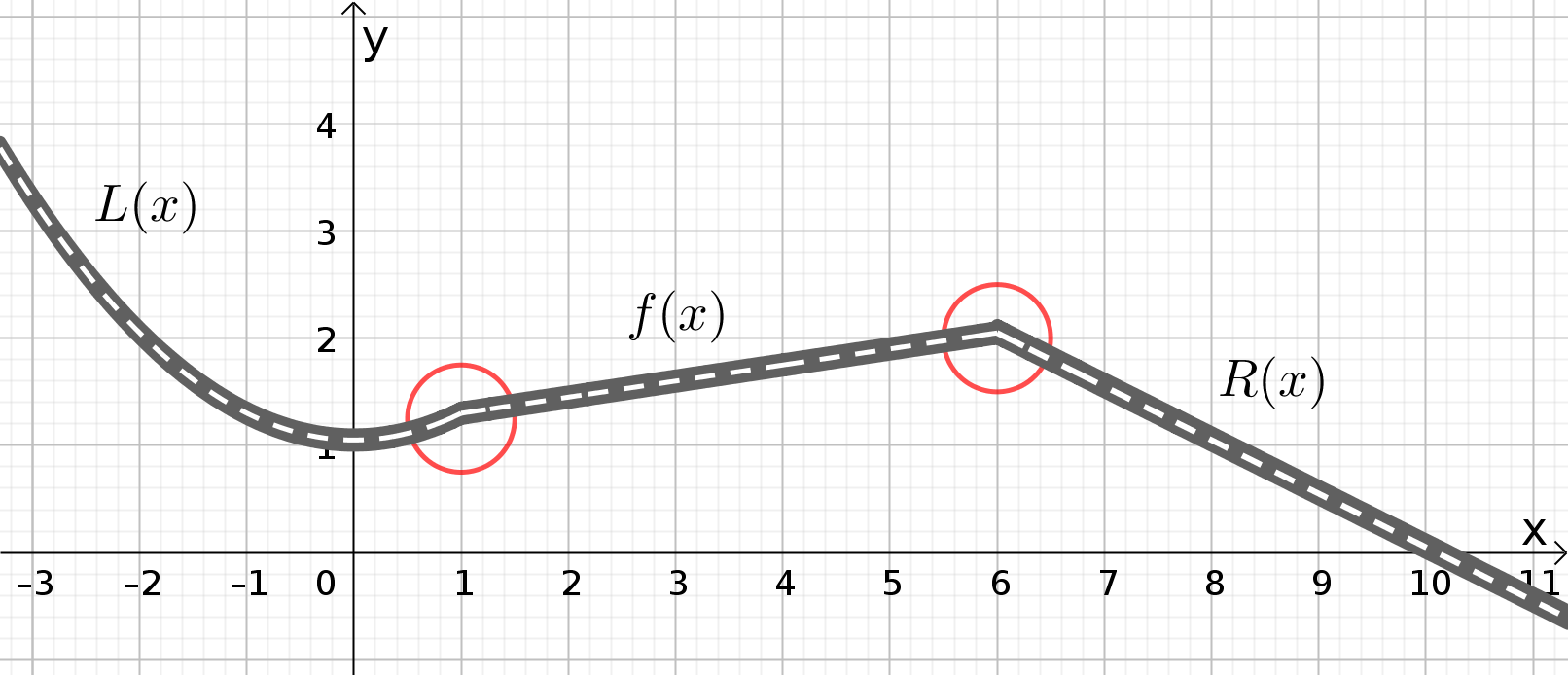
Auch das wäre keine optimale Lösung. Die Autos könnten nun zwar von L(x) auf das Straßenstück R(x) gelangten, aber bei höheren Geschwindigkeiten wird es an den Übergangsstellen sicherlich zu Unfällen kommen, weil es dort einen Knick gibt. Daher muss für solche Trassierungen eine weitere Bedingung erfüllt sein:
Knickfreiheit - Gleichsetzen der ersten Ableitung
Wenn die aneinander anschließenden Straßenstücke ohne Knick, also glatt, in einander übergehen sollen, dann müssen sie an den Übergangsstellen die gleiche Steigung haben. Die Steigung einer Funktion an einer Stelle x berechnet man mit der ersten Ableitungsfunktion. Also müssen für Knickfreiheit folgende beiden Bedinungen eingehalten werden:
Mit den beiden Bedingungen aus der Versatzfreiheit haben wir nun also 4 Bedingungen und können somit eine Verbindungsfunktion f(x) finden, die eine ganzrationale Funktion 3. Grades ist.
nach einer Funktionssynthese sieht das z.B. so aus:
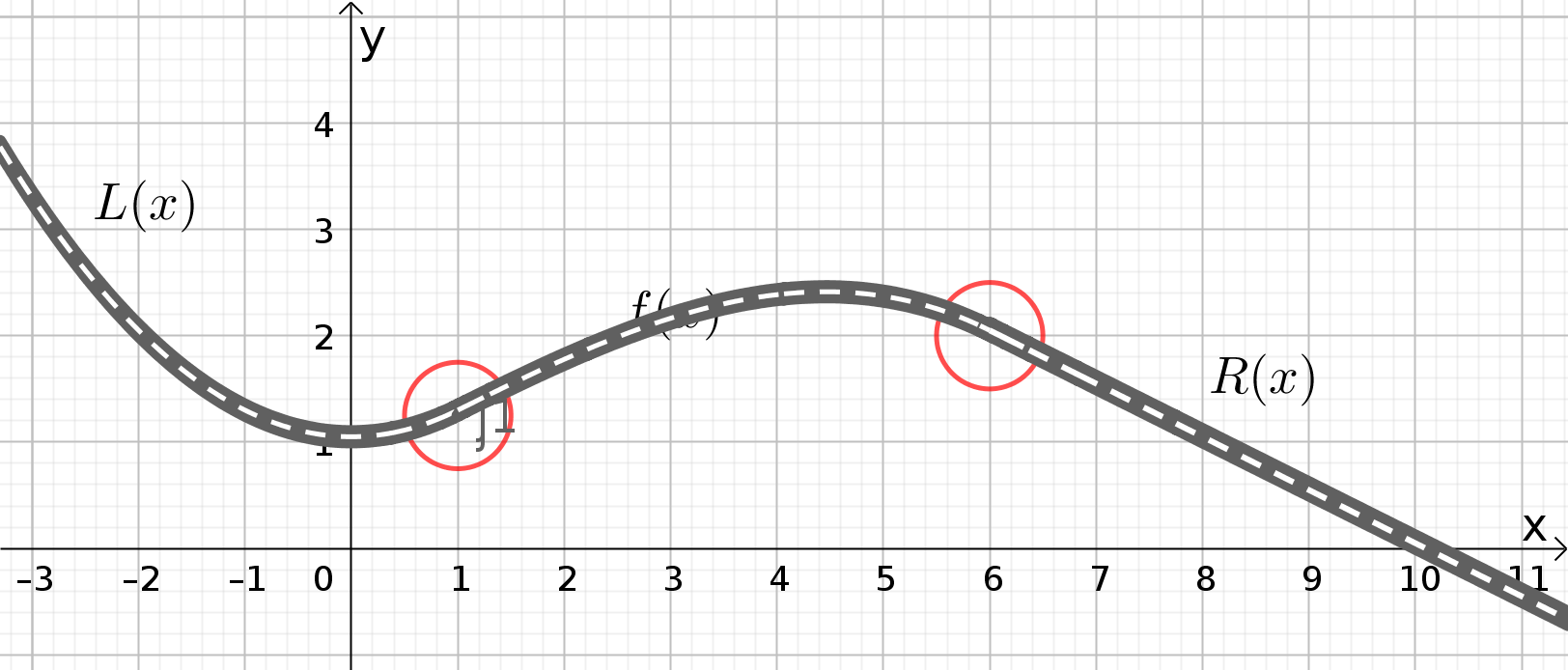
Das sieht doch nun schon viel besser aus, so würden einige vielleicht schon ihre Straßen bauen. Allerdings gibt es immer noch ein Problem, dass man hier nicht so richtig sehen kann, das man aber spührt, wenn man tatsächlich am Lenker eines Autos sitzt. Wenn eine Kurve knickfrei ist, dann kann sie trotzdem an den Übergangsstellen sehr plötzlich die Krümmung wechseln. An dem rechten Anschluss zum Beispiel ist R(x) eine gerade Straße, die gar keine Krümmung besitzt, und eine "krumme" Straße führt hinein. Für den Fahrer heißt das, dass er pötzlich das Lenkrad herumreißen muss, um der Straße zu folgen. Auf der linken Seite geht im Anschlusspunkt sogar eine Links- in eine Rechtskrümmung über. Auch hier würde ein Autofahrer plötzlich das Lenkrad herumreißen müssen, um dem Straßenverlauf zu folgen. Daher müssen auch die Krümmungen der Kurvenstücke einander angeglichen werden:
Krümmungsruckfreiheit - Gleichsetzen der zweiten Ableitung
Ich weiß nicht, ob das Wort krümmungsruckfrei wirklich von Ingenieuren verwendet wird, aber es ist hilfreich ein Wort für diese Eigenschaft zu haben. Und in den Schulbüchern hat sich krümmungsruckfrei dafür durchgesetzt.
Wir haben schon in Kapitel 7.2 festgestellt, dass die zweite Ableitung viel über die Krümmung einer Funktion verrät. Wenn die Knickfreiheit gewährleistet ist, und dann auch noch die zweite Ableitung der beiden Anschlussstücke den gleichen Wert hat, dann haben diese beiden Straßenverläufe an dieser Stelle sogar den gleichen Krümmungsradius, denn dieser lässt sich aus der ersten und der zweiten Ableitung einer Funktion berechnen. Also müssen für Krümmungsruckfreiheit zur Versatz- und Knickfreiheit noch zwei weitere Bedingungen hinzugefügt werden:
Nun haben wir schon 6 Bedingungen, die wir an eine Funktion stellen müssen, damit sie im Straßenbau eine vernünftige Lösung ist. Das heißt man benötigt eine ganzrationale Funktion 5. Grades, um ein geeignetes Straßenstück zu finden. Nach einer Funktionssynthese, sieht das in diesem Beispiel so aus:
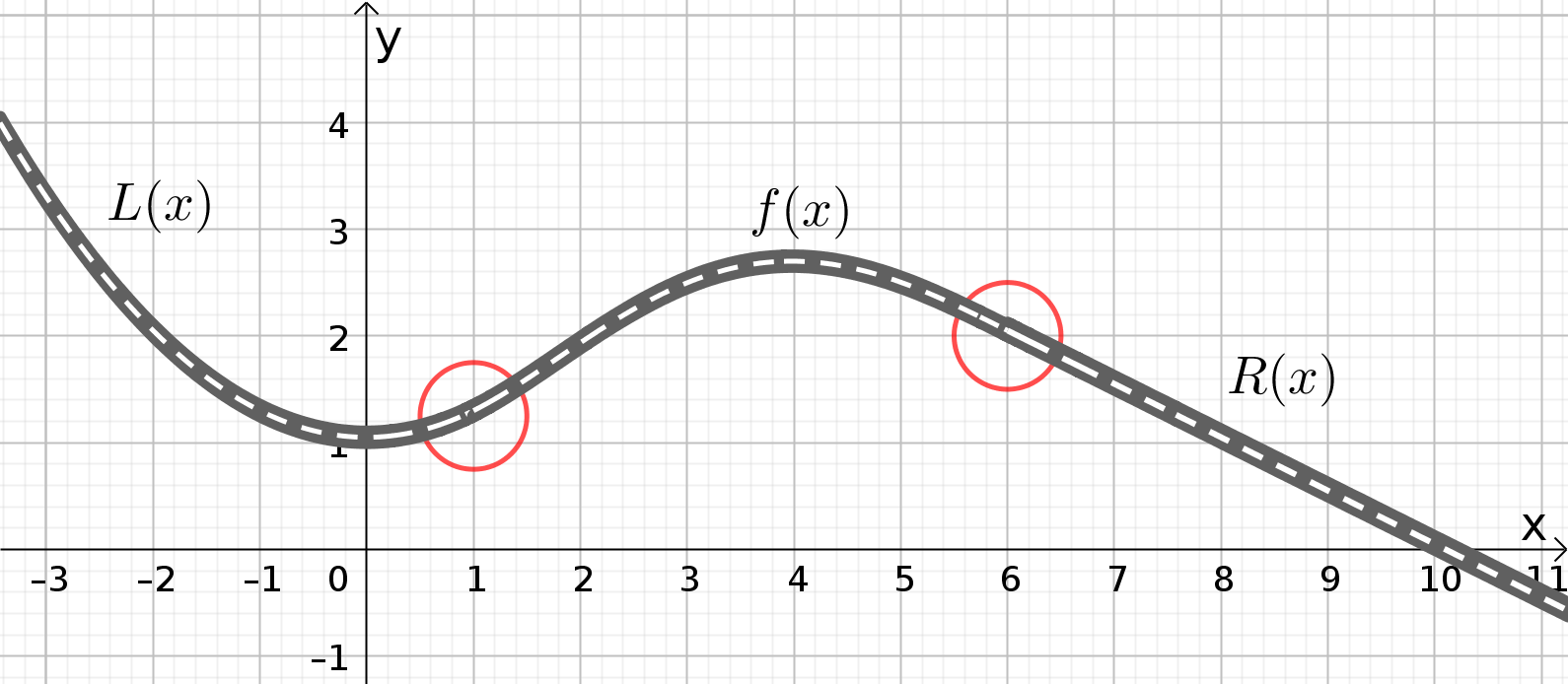
Diese Straße ist nun sogar etwas länger geworden, als die, die nur knickfrei war. Aber diese paar Meter Straße können in diesem Zusammenhang Menschenleben retten. Nun kann man auch mit höherer Geschwindigkeit ohne ruckartig am Lenkrad reißen zu müssen vom Straßenstück L(x) über das Stück f(x) in das Straßenstück R(x) fahren.