1 Einheiten und Größenordnungen
Die Wissenschaftler haben sich weltweit auf die gleichen Einheiten für ihre physikalischen Größen geeinigt. Dieses internationale Einheitensystem nennt sich SI. Das kommt aus dem Französischen für "Système international d’unités".
Die sieben SI-Basiseinheiten
Es gibt genau 7 Basiseinheiten, aus denen alle anderen bekannten Einheiten zusammengesetzt sind:
| Basisgröße | Größensymbol | Einheit | Einheitenzeichen |
|---|---|---|---|
| Länge | l | Meter | m |
| Masse | m | Kilogramm | kg |
| Zeit | t | Sekunde | s |
| Stromstärke | I | Ampere | A |
| Temperatur | T | Kelvin | K |
| Stoffmenge | n | Mol | mol |
| Lichtstärke | Iv | Candela | cd |
Da es in Druckschrift etwas schwer zu erkennen ist: Das Symbol für die Länge ist ein kleines L und das der Stromstärke ist ein großes i. Auch die Lichtstärke ist ein großes i mit dem Index v: IV.
Null Grad Kelvin ist der sogenannte absolute Temperaturnullpunkt. Bei dieser Temperatur würde sich nichts mehr bewegen. Null Grad Celsius sind 273,15 Grad Kelvin.
Man muss zu einer Tempratur in Grad Celsius nur 273,15 dazurechnen, um die Temperatur in Kelvin zu erhalten. Hier einige Beispiele:
0°C = 273,15 K
1°C = 274,15 K
10°C= 283,15 K
100°C = 373,15 K
Größenordnungen und Zehnerpotenzen
Oft ist es gar nicht so wichtig, wie groß eine Zahl genau ist. Es reicht wenn man weiß, mit welcher Größenordnung man es zu tun hat. Darum werden sehr große und sehr kleine Zahlen in der Physik mit Hilfe von Zehnerpotenzen geschrieben, wobei die Zehnerpotenzen nur die Größenordnung angeben, in dem sich die Zahl befindet:
Zehnerpotenzen
positive Exponenten sind große Zahlen

negative Exponenten sind kleine Zahlen
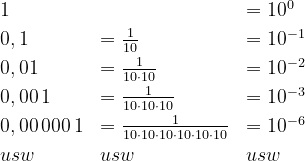
Gleitkommaschreibweise
Zahl = m · 10n für große Zahlen oder Zahl = m · 10- n für kleine Zahlen. Dabei ist m (die Mantisse) in der Regel eine Zahl zwischen 1 und 10 und n eine positive ganze Zahl. Sehen wir uns einige Naturkonstanten als Beispiel an:
Große Zahlen
Die Lichtgeschwindigkeit im Vakuum ist
c = 299792458 m/s ≈ 300 000 000 m/s= 3 · 108 m/s
Die Lichtgeschwindigkeit beträgt also etwa 3 · 108 m/s. Diese Angabe kann man sich gut merken und sie weicht nur um 0,07% vom genauen Wert ab. Und mit etwas Übung sieht man sofort, dass die Größenordnung Hundert Millionen ist, das Licht ist also ganz schön schnell.
Kleine Zahlen
Die Masse von Atomen werden oft in der atomaren Masseneinheit u angegeben. Ein u ist u ≈ 1.660 · 10-27 kg, das ist genau ein 12tel der Masse eines Kohlenstoffatoms C12 oder etwa das Gewicht eines Protons oder eines Neutrons, den Bausteinen aus denen unsere Atomkerne bestehen. Ohne Zehnerpotenz geschrieben ist eine atomare Einheit gleich
u ≈ 0,00 000 000 000 000 000 000 000 000 166 kg
Man sieht hier sofort, dass es viel angenehmer ist, solche Zahlen mit Größenordnngen zu schreiben.
Wie bestimmt man eine Größenordnung aus einer Dezimalzahl?
Große Zahlen
300 000 000 = 3 · 10⁸
123 456 7 = 1,234567 · 106
920 000 000 000 = 9,2 · 1011
12 345,67 = 1,234567 · 104
Der Exponent für die Größenordnung ist die Anzahl der Ziffern bis zum Dezimalkomma (falls vorhanden) minus Eins.
Kleine Zahlen
0,00 00432 = 4,32 · 10-5
0,00 000 000 000 789 123 = 7,89 123 · 10-12
Der Exponent für die Größenordnung ist die negative Anzahl der Nullen bis zur ersten Ziffer, die keine Null ist. Dabei muss die Null vor dem Komma mitgezählt werden.
Ein kleines Übungsprogramm dazu:
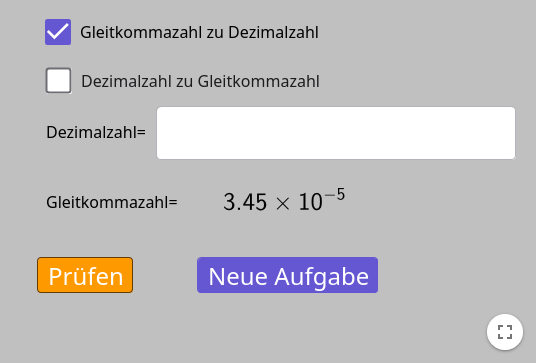
Rechnen mit Zehnerpotenzen
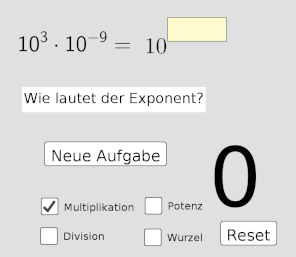
Das Multiplizieren, Dividieren, Potenzieren und Wurzelziehen ist mit Zehnerpotenzen auch ganz einfach.
Auch dazu gibt es ein Programm zum Üben:
SI-Vorsilben
Um einen schnellen Überblick zu bekommen, werden besonders häufig Größenordnungen verwendet, die ein Vielfaches der Zahl 1000 sind. Diese Größenordnungen haben daher einen Namen bekommen: "Kilo" heißt 1000, und "Mega" steht für 1000 000. Eine Tabelle mit allen internationale gebräuchlichen Namen ist hier (www) zu finden.
Einige dieser Silben haben wir schon so häufig im Sprachgebrauch, dass viele gar nicht mehr wissen, was sie eigentlich bedeuten: Ein Kilogramm sind 1000 Gramm. Ein Zentimeter ist ein hundertstel und ein Millimeter ist ein tausendstel Meter.
Große Zahlen
| Symbol | Name | Zehnerpotenz | Dezimalzahl |
|---|---|---|---|
| k | Kilo | =10³ | =1 000 |
| M | Mega | =10⁶ | =1 000 000 |
| G | Giga | =10⁹ | =1 000 000 000 |
| T | Tera | =10¹² | =1 000 000 000 000 |
| P | Peta | =10¹⁵ | =1 000 000 000 000 000 |
Kleine Zahlen
| Symbol | Name | Zehnerpotenz | Dezimalzahl |
|---|---|---|---|
| c | Zenti | =10⁻² | =0,01 |
| m | Milli | =10⁻³ | =0,00 1 |
| µ | Mikro | =10⁻⁶ | =0,00 000 1 |
| n | Nano | =10⁻⁹ | =0,00 000 000 1 |
| p | Piko | =10⁻¹² | =0,00 000 000 000 1 |
| f | femto | =10⁻¹⁵ | =0,00 000 000 000 000 1 |
Was muss ich wissen?
- Ich kenne die sieben SI-Basiseinheiten
- Ich muss große und kleine Zahlen als Gleitkommazahl schreiben können
- Ich muss Zahlen in Gleitkommadarstellung als normale Dezimalzahl schreiben können
- Ich kenne die Namen und die Symbole für die Größenordnungen für Tausend, eine Million und eine Milliarde
- Ich kenne die Namen und die Symbole für die Größenordnungen für ein Tausendstel, ein Millionstel und ein Milliardstel
______
zurück
Backlinks:
2 Physikbücher:Naturwissenschaften für die FSP
2 Physikbücher:Naturwissenschaften für die FSP:8 Zustandsgleichung für ideale Gase
