5.4 Energie eines Kondensators
Für Kondensatoren gilt 
bzw. 
.
Für elektrische Energie gilt allgmein 
.
Aber bei Kondensatoren sind die Ladung Q und die Spannung U von einander abhängig. Das lässt sich in einem Funktionsgraphen darstellen:
Wenn nur eine kleine Spannung anliegt, dann ist auch die Ladung auf den Kondensatorplatten klein und dann ist auch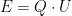 
klein. Je größer die Spannung, desto größer ist auch der Energiezuwachs. Grafisch bedeutet das, dass die Energie die Fläche unter dem Funktionsgraphen von Q(U) ist. Bei der Spannung U1 hat der Kondensator die Ladung Q1 = C · U1
Damit ist die Fläche unter dem Graphen und somit auch die Energie gleich: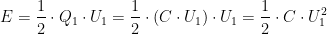 
.
Allgemein gilt daher für die Energie, die in einem Kondensator gespeichert wird:
Mit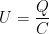 
kann man die Energie auch in Abhängigkeit von Q ausdrücken:
Dieser Zusammenhang wird allerdings selterner benötigt.
Beispielaufgabe
In einem Fahrradrücklicht wird ein Kondensator von C = 1F verwendet. Der Dynamo liefert eine Spannung von U=6V. Wie viel Energie kann mit diesem Kondensator gespeichert werden?
Lösung:
Backlinks:
2 Physikbücher:BGPhysik12-1:5 Der Kondensator