1.3 Die Ableitungen der Schwingungsfunktion
In der Physik gilt grundsätzlich:
Wenn wir eine Funktion s(t) des Weges in Abhängigkeit von der Zeit haben, dann ist die erste Ableitung dieser Funktionsgleichung die Funktion für die Geschwindigkeit v(t) in Abhängigkeit von der Zeit:
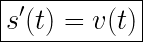
Wenn wir eine Funktion s(t) des Weges in Abhängigkeit von der Zeit haben, dann ist die zweite Ableitung dieser Funktionsgleichung die Funktion für die Beschleunigung a(t) in Abhängigkeit von der Zeit:
Dies gilt grundsätzlich, also nicht nur für Schwingungsgleichungen.
Bei der Ableitung einer Schwingungsfunktion muss die Kettenregel der Differentialrechnung angewendet werden:
Ist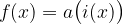 
, dann ist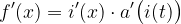 
Eine Schwingungsgleichung (ohne Offset) lautet:
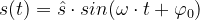
Äußere Funktion:
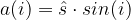
Ableitung der äußeren Funktion:
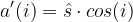
Innere Funktion:
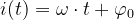
Ableitung der inneren Funktion:
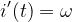
Damit ist
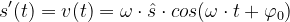
Mit cos'(x)=-sin(x) gilt dann für die zweite Ableitung:
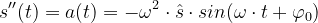
Daraus folgt die
Differentialgleichung für harmonische Schwingungen
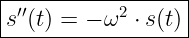
Ableiten von Schwingungsgleichungen üben:
Klicken Sie auf das Bild unten und Sie werden auf eine Geogebra-Seite weitergeleitet, auf der Sie das Ableiten von Schwingungsfunktionen üben können.
Backlinks:
2 Physikbücher:BGPhysik12-2:1.1 Schwingungen - Einführung